04 Сен 12 ОСНОВЫ МАТЕМАТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ДИСПЕРСИОННОГО АНАЛИЗА

При изучении свойств дисперсных материалов, а так­же при разработке способов их получения и использова­ния часто возникает необходимость в выявлении закоио - мерностей распределения частиц по их размерам. Нали­чие таких закономерностей в порошках определенных классов, (позволяющих аппроксимировать кривые распре­деления математическим выражением, было неоднократ­но отмечено на основании многочисленных эксперимен­тальных данных. Математическая форма записи «ривых распределения практически удобнее .графической и поз­воляет производить корректное сравнение дисперсных характеристик, полученных разными методами дис­персионного анализа. Аналитические выражения об­легчают экстраполирование кривых, вычисление средних характеристик и расчет удельных поверхностей порош­ков. Стремление выявить закономерности распределения обусловлено также необходимостью в ряде случаев опи­сания дисперсности порошков ограниченным числом па­раметров. Это особенно важно при сравнительном ана­лизе процессов и аппаратов, предназначенных для полу­чения и переработки порошков.

Как указывалось, порошок представляет собой набор частиц различной массы и геометрической формы. Их размеры ограничены как со стороны верхнего, так и со стороны нижнего значения их масс, что обусловлено осо­бенностями приготовления и свойствами высокодисперных материалов. Очень большие и очень «малые частицы не по­падают в порошок в результате естественных или искусст­венных классификационных процессов. Даже при отсут­ствии классификации существование предельно малых частиц ограничивается термодинамическим стремлением их к взаимному слиянию — аг регации.

Кроме массы, частицы можно охарактеризовать объе­мом, плошадью поверхности и размером. Как уже ука­зывалось выше, для частиц произвольной формы эти четыре характеристики, вообще говоря, не связаны од­нозначно между собой. Однако обычно в реальных по­рошках соблюдается геометрическое подобие (хотя бы статистически усредненное) формы зерен различных раз­меров. Это обстоятельство позволяет установить взаимо­связь 'между массой, объемом, площадью поверхности и определяющим размером зерна. В дальнейших расчетах будет принято, что частицы твердых тел однозначно ха­рактеризуются их массой (М0), объемом (v), площадью поверхности (5) и размером (Х=2г), причем: 5 = рХ2; M0=Dd; и = аЛ'3, где D — плотность вещества, а и р — численные коэффициенты. При эгом принимают, что частицы однородны по составу и не имеют внутренних полостей. Размер частиц X может быть определен в каждом конкретном случае по-разному в зависимости от их формы, практического применения порошков и спо­соба их дисперсионного анализа.

Распределение частиц по размерам является наибо­лее полной дисперсионной характеристикой. Это особен­но справедливо для однородных по составу, непористых и не слишком шероховатых зерен правильной или почти правильной формы. Поскольку число частиц в порошках обычно очень велико, для аналитического описания рас­пределения частиц по размерам возможно привлечение дифференциального и интегрального исчисления, опери­рующих понятиями бесконечно малых. Применительно к порошкам под числом частиц dN обычно подразуме­вают некоторое небольшое число частиц из общего чис­ла их N (причем dN очень мало ио сравнению с N), раз­меры которых отличаются. не более чем на dX. Значения дифференциала массы, объема, площади поверхности определяются аналогично.

Статистика дисперсных систем, в частности порош­ков, довольно хорошо изучена в экспериментальном от­ношении. Из многочисленных наблюдений известно, что функция распределения частиц по их размерам в боль­шинстве случаев имеет один хорошо выраженный мак­симум асимметричной формы с крутым спадом в сторо­ну мелких и пологим — в сторону крупных частиц. Были сделаны неоднократные попытки математического опи­сания (правда, без уяснения физического смысла) кри­вых распределения.

Асимметричные кривые. распределения частиц в об­щем случае описываются уравнением вида:

*«акс-*ми„ - Г'** (1)

Где F |(ц)—логарифмически нормальная. функция ц; X— размер частиц, изменяющийся В пределах Лмиі!<Л'<Л'маис-

Практическое использование уравнения (1), называ­емого. иеидеальным логарифмически нормальным зако­ном, довольно сложно. Поэтому, учитывая, что нижний предел размеров частиц, особенно для высокодисперсных материалов, очень мал и практически определить его невозможно, обычно принимают Хми„=0. Учитывая так­же, что спад кривой F(X) в области крупных частиц до­вольно плавный, для опнсання кривой распределения в области X Лмакс можно принять /г(р)=/г(Х). Таким образом, кривая распределения частиц но размерам ап­проксимируется логарифмически нормальным законом, впервые выведенным применительно к продуктам разру­шения твердых материалов Колмогоровым.

Логарифмически нормальный закон весового распре­деления частиц по их размерам имеет вид:

X

М, пт

ВД. о - • 2

Где А— постоянная нормировки;!—медиана; о — дисперсия распределения.

В тех же предположениях относительно предельных размеров частиц дифференциальная кривая распределе­ния может быть аппроксимирована и степенным выра­жением, которое в наиболее общей форме записывают как:

FC(X) = А Хт ехр (— <х Хр), (3)

Где т=т0+п.

Параметры т0, а, р определяют характер распреде­ления, остроту. максимума и степень асимметрии кривой,

DN

А п — его вид. Так, если F(X)= ^ представляет

Собой распределение числа частиц по размерам, то т —

DS

— гп0\ если Г(Х) = cix" —распределение поверх­ня;

Ностей, то т—іщ-\-2; если F(X)= dX ■ —распреде­ление частиц по массам или объемам, то m=m0+3. В такой записи величина т0 определяет только особеннос­ти распределения исследуемого порошка. Величину А выбирают обычно так, чтобы F(X) было выражено в до­лях единицы или в процентах на единицу размеров.

Выражение (3) обобщает ряд известных аналитиче­ских форм записи кривых распределения. Так, при т0—О и р=\ оно превращается в уравнение Мартина, при т0=0 — в уравнение Хейвуда, при /3=0 — в уравнение Го дена и Андреева, при т0—0 и р=2— в нормальное распределение Гаусса, при т0=р = а — в уравнение Ро - зина и Раммлера. Аналогично получаются и многие дру­гие функции распределения, в которых параметры а,

(2)

Т0 и р не зависят от размера частиц. Все они отличают­ся между собой тем, что описывают распределения. раз­личной степени асимметрии и крутизны максимума.

Столь же широкой общностью, как и формула (3), обладает и формула Свенсона, которая в принятых здесь обозначениях в дифференциальной форме может быть записана в виде:

(4)

F(X) = А ехр

-шжг

Где п, р, XD — параметры распределения

Формулы (2) — (4) обобщают все известные функ­ции распределения.

Экспериментальные исследования гранулометричес­кого состава порошков показали возможность их описа­ния в одних случаях логарифмически нормальным, в дру­гих— различными степенными законами. В дальнейшем Авдеевым [II] было доказано, что при надлежащем вы­боре параметров степенные законы (3) и (4) вполне пригодны для описания кривых распределения, к кото­рым ранее применяли логарифмически нормальный за­кон. При этом оказалось, что наибольшее практическое приложение из всех частных выражений степенного за­кона имеет уравнение Розина — Раммлера. Поскольку параметры всех уравнений определяются по эксперимен­тальным данным, с практической точки зрения предпоч­тение должно быть отдано простейшему из них.

В тех случаях, когда распределение частиц по разме­рам имеет два и более максимума, их аналитическое описание становится довольно сложным. Авдеевым по­лучено аналитическое выражение кривых F(X) в виде степенного многочлена и разработана система опреде­ления их параметров. Аналогичное описание кривых распределения многочленом, каждое слагаемое которого является уравнением Розина — Раммлера, предложено Роузом [5]. Как и у Авдеева, число слагаемых много­члена равно числу максимумов кривой распределения.

Все .приведенные здесь формулы нормируются для

Определения постоянной А, так чтобы J F (X)dX= 1. В

О

Этом случае нормировка по уравнению (3) дает

MH 1

[.-mr.

/т + 1\

Где Г I — гамма-функция

\ Р /

В зависимости от вида кривой распределения посто­янная А выражает приведенное к единице либо общее число частиц (m=m0), либо суімму диаметров (m = m0+ + 1), либо суммарную поверхность (m = m0-f-2), либо суммарный объем или вес (m = m0+G) всех частиц исследуемой. пробы порошка.

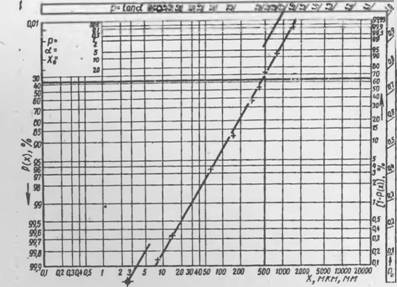
Для вычисления параметров логарифмически нор­мального распределения по экспериментальным данным удобно представить их в вероятностно-логарифмических координатах. Для изображения дифференциальной кри­вой по оси абсцисс откладывают \пХ, а по оси орди­нат— значение функции Гаусса от 1пЛ", для интеграль­ной кривой абсцисса—lnX, а ордината—интеграл вероят­ности. В тех случаях, когда кривые распределе­ния аппроксимируются логарифмически нормаль­ным законом, в таких координатах они будут изоб­ражены в виде прямых. Действительно, в прежних обоз­начениях содержание частиц с размерами, большими данного, может быть выражено:

Р (X) = А | exp I------ —- z21 dz — j4erf (X), (5)

Х L 2 J

1 , Л

Где Z = ——\n —.

О I

DP

В такой замене F(z)— —функция Гаусса.

Если Р(Х) выражено в долях единицы, а 0<Х<оо, то А = 2. Для построения шкалы по оси ординат следует воспользоваться таблицей ■ интеграла вероятности. На рис. 1 показана рассчитанная таким путем координат­ная сетка.

'По определению медиана £ равна такому размеру частиц, для которого Р(£)=0,5, т. е. половина всего ко­личества частиц имеет размер больше, половина — меньше g. Это определение не зависит от вида функции F(X). Поэтому значение £ легко находят по графику Р(Х) или F{X) в любых координатах. Тангенс угла нак­лона прямой в вероятностно-логарифмических координа­тах равен дисперсии о.

Если определена медиана, дисперсию можно найти и по какой-либо точке кривой, для которой Р(Х)ф 0,5, т. е. In 0. Для этого по таблицам интеграла ве­

Роятности находят значение z, соответствующее выбран-

__ 1 X

Ному Р(Х). Затем вычисляют а = г •

По вычисленным параметрам |ия можно найти и ос­тальные характеристики распределения. Так, средний

— 00 / о \2

Размер частиц Х=j AT^X) J*=gexp(——J всегда боль­ше значения медианы. Мода распределения, т. е. значение X, при котором F(X) имеет максимум, £=£ехр (—о2) всегда меньше значения медианы.

Распределение числа частиц по размерам также мо­жет быть аппроксимировано логарифмически нормаль­ным законом и отличается оно от весового распределе-

І

Ния только значением медианы, дисперсия же их одина­кова. Поэтому в вероятностно-логарифмических коорди­натах оба вида распределения изображаются парал­лельными линиями Этот вывод следует из особенностей логарифмически нормальной функции. Действительно:

' (в)

Кроме логарифмически нормального распределения, как уже указывалось, кривые гранулометрического сос­тава часто неплохо описываются уравнением Розииа — Раммлера, которое в дифференциальной форме (распре­деление объемов или масс) удобно записать в виде:

F (X) — ар А 1 ехр (-аГ).

Для определения параметров распределения аир выгодно использовать интегральную характеристику — содержание частиц с размерами больше данного 00

Р(Х)~ f F(X)dX--= Аекр (—?ХР).

Х

При Х=0 будем считать, что Р(0) = 1, т. е. суммар­ное'содержание всех частиц равным 1, тогда А — 1 и Р(Х) =ехр (—аХг).

Для определения аир графически кривую распреде­ления удобно изобразить в двойном логарифмическом масштабе

In In - j = In a + P In X. . (7)

1

Уравнение (7) в координатах lnX — абсцисса, Inln — —

Ордината представляет собой прямую, тангенс угла нак­лона которой равен р, а отрезок, отсекаемый иа оси ор­динат,— lna (рис. 2).

Уравнение Розина — Раммлера удобно представить в виде:

(И-Ш

J X" ехр

В такой интерпретации при любом значении р вели­чину параметра Хв определяют из условий Х=Х0 и

Р=е~т. е. содержание частиц с размерами, большими Х0, составляет е~1 =0,368.

Величина Х0 характеризует дисперность продуктов измельчения, которая тем выше, чем меньше значение Хо;

Рис 2 Координатная сетка по степенному распределению Розина — Раммлера

Р характеризует дисперсию распределения, которая тем больше, чем меньше значение р.

Распределение объемов частиц по размерам в такой записи имеет вид:

При условии, что Р>1, эта функция имеет в точке (мо­да) у/~^.максимум; экспериментальные значения

Р не могут быть меньше 1, поскольку на опыте функции распределения всегда имеют максимум.

Медиана распределения £ может быть найдена из ус-

— ловия 30

Р exp [_ (і - J = 0,5, т. е. ? = Х0 Г In 2. (8)

Среднее значение размера по распределению Рози - на — Раммлера:

I

При /?>1 в такой записи Г( ~+1) мало отличается от

1. Так, при р=2 Г(1,5) минимально и равно 0,89, при р= 1 значение Г (2) = I При всех других значениях \<р<. оо значения гамма-функции находятся в преде­лах 0,89<Г<1.

Величины среднею размера, моды и медианы, как это следует из формул (8) и (9), близки между собой. Так, при р=2, что встречается довольно часто, t,=0,7 LY0; £ = 0,83*о; Х=0,89Х0-, при р = 3 £;=0,88Х0; | = 0,88Х0; X—0,89Х0.

Средние значения могут быть рассчитаны не только по аналитическому выражению распределения частиц по размерам, іно и непосредственно из экспериментальных данных. При этом, как и при аналитических расчетах, можно применять различные виды средних значений, выбор которых диктуется конкретными условиями экс­перимента (табл. 2) Данные таблицы четко иллюстри­руют резкое несовпадение численных значений различ­ных средних.

Часто в практической работе возникает необходи­мость определения по данным гранулометрического сос­тава удельной поверхности порошков. Если функция F(X)—весовое распределение частиц по размерам, то удельная поверхность порошка равна:

Я

6 е м? кс

S = V^L=p j X-lF(X)dX, (10)

/ ' х

Мин

Где 5 — выражено в единицах площади на единицу веса.

Отношение численных коэффициентов поверхности к объему частиц (Р) для шара и куба с гладкими стенка­ми равно 6. Для частиц измельченных материалов, фор­ма которых отлична от правильной, а поверхность не­ровная, это отношение может быть значительно больше 6, часто в 2—4 ,раза. Величина р зависит от природы ма-

Таблица 2 Формулы для расчета средних размеров частиц [7] Среднее Формула Значение среднего в мкм (пример) Арифметическое Лі + Х2 2 91 2 л, Xt Ъ п{ 23,12 Геометрическое .Vxlx3 2,78 По площади частиц 2 пе X) 2 л, Xt 0,22

4,86

По удельной поверхности

0,127 0,127

34,96

Хп, X]

По объему частиц

0,43

2/1,

V

(99 "%Рчастиц Меньше * ZSSS? р^мТа,- V »аэмеР зеРеи

<0.,* чаотиц «еиьше данного „й®, ^ГТрГ даи^іра^и: S— удельная поверхность фракции.

Териала, способа его измельчения, размера частиц и должна быть определена прямыми измерениями в каж­дом конкретном случае. С этой целью можно, например, •воспользоваться измерением площади поверхности ка­кой-либо фракции одним из сорбционных методов. Фор­мула (10), в. которой gi — весовое содержание фракции частиц с размерами X,- (в долях единицы), удобна для вычисления уделыюн поверхности но экспериментальным измерениям гранулометрического состава. Интеграль­ную формулу <Ю) применяют в тех случаях, когда зна­чение F(X) дано в аналитическом виде. Для сферических частиц

Л£ і л,-

В многих случаях можно полагать, что значение Э от размеров частиц не зависит, формы для негладких или несферических часгиц значе­ние удельной поверхности

. S-P'SC (")

/ Л/

Равно:

Тогда с учетом фактора Таблица 3 Фактор формы различных дисперсных материалов

	Фак­	Удель­
Материал	Тор, Формы р "	Ный Вес V
Пыль ......	2,28	2,28
Стекло. . . .	1.9	2,57
Слюда	9,27	2,8
Уголь	2,12	1.3
Пробка...................	1,98	0,3
Кварц	1,43	2,64
Вольфрам	1,18	17,3

* Условия применения величины Р': р' = Р/6: 5 = -1Ё1 .

Для вычисления удель­ной поверхности по экспери­ментально измеренной кри­вой распределения график следует разбить на интерва лы и взять по ньм сумму в соответствии с формулой (11). Значення фактора фор­мы ряда материалов приве­дены в табл. 3. Как следует из данных табл. 3, значе­ния фактора формы суще­ственно превышают единицу, особенно для такого ма­териала, как слюда с резко выраженной анизометрично - стью частиц.

33

Подсчитаем удельную поверхность, предполагая справедливым распределение Розшна — Р. аммлера

З Зак 102

Значение гамма-функции находят из стандартных таб­лиц для заданного р, измеренного по эксперименталь­ным данным. Если таблицы содержат значения гамма - функции только в пределах изменения аргумента от 1 до 2, то для 1<р<2 следует воспользоваться тем, что Г (т+1)=тГі(т):

Рг (з-—)

\ Р )

О

Для р = 2 Г (2------ ) = 1, а для р>2 значение гамма-

Р

Функции нигде не становится меньше 0,89, и. величина удельной поверхности близка к вычисленной по харак­теристикам распределения імоде, медиане или среднему. Такое положение можно считать справедливым с доста­точной в практических расчетах степенью приближения для всех р>1,5 (Г=»1,3). Даже для р=1,3, Г (2— 2

— —Это означает также, что для достаточно

Узких распределений с малой дисперсией (р>1,5) по удельной поверхности можно приближенно оценить х а р акте р истики р аюп редел єни я.

Если же р приближается к 1, что означает расшире­ние кривой, оклад мелких фракций /в общем содержа­нии частиц возрастает, а удельная поверхность стре­мится к бесконечности. Причина такого расхождения кроется, возможно, в несоответствии распределения закону Розина — Раммлера, в котором предполагает­ся, что нижняя граница размеров частиц равна нулю. Это предположение. применительно ко всем порошкам без исключения івряд ли 'может быть оправдано.

Для случая применимости логарифмически нормаль­ного распределения, нормированного. к единице, в соот­ветствии с формулой (10) и с учетом выражений (5) и (6), а также считая, что пределы изменения размеров частиц (0, ), для удельной поверхности (на единицу объема) получим выражение

Р •